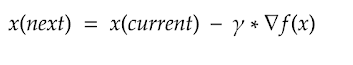This document is an electronic record in terms of Information
Technology Act, 2000 & rules thereunder as applicable and the
amended provisions pertaining to electronic records in various
statutes as amended by the Information Technology Act, 2000. This
electronic record is generated by a computer system and does not
require any physical or digital signatures. This document is
published in accordance with the provisions of Rule 3 (1) of the
Information Technology (Intermediaries guidelines) Rules, 2011
that require publishing the rules and regulations, privacy policy
and Terms of Use for access or usage of www.tresndive.com. Please
read the following terms and conditions very carefully as your use
of service is subject to your acceptance of and compliance with
the following terms and conditions ("Terms"). By subscribing to or
using any of our services you agree that you have read, understood
and are bound by the Terms, regardless of how you subscribe to or
use the services. If you do not want to be bound by the Terms, you
must not subscribe to or use our services.
Introduction
Welcome to the ceduratech.com ("Website" or "ceduratech.com")
service provided by CEDURA Testsol Pvt. Ltd. . This
website/app/chatbot is owned and operated by CEDURA Testsol Pvt.
Ltd. ('we' or 'us' or 'SSL'). Registered office: Hyderabad,
Telengana). In using the ceduratech.com service, of CEDURA Testsol
Pvt. Ltd you are deemed to have accepted the Terms and Conditions
of the agreement listed below or as may be revised from time to
time, which is, for an indefinite period and you understand and
agree that you are bound by such terms till the time you access
this website/app/chatbot. If you want to ask us anything about
these terms & conditions or have any comments or complaints on or
about our website/app/chatbot, please write to us at
hello@ceduratech.com
Payment Terms
You agree to pay the price applicable for the product or service
on our website/app/chatbot (CEDURA Testsol Pvt. Ltd.
) and the CEDURA Testsol Pvt. Ltd. mobile applications for
shopping at the time you submitted your order (product or service
price). All payments are non-refundable (except as expressly set
forth in the Terms and Conditions.
Ownership of Rights
All rights, including copyright, in this website/app/chatbot are
owned by or licensed to CEDURA Testsol Pvt Limited. Any use of
this website/app/chatbot or its contents, including copying or
storing it or them in whole or part, other than for your own
personal, non- commercial use is prohibited without the permission
of CEDURA Testsol Pvt Limited. You may not modify, distribute or
re-post something on this website/app/chatbot for any purpose.
Accuracy of Content and Invitation to Offer
CEDURA has taken every care in the preparation of the content of
this website/app/chatbot, in particular to ensure that prices
quoted are correct at time of publishing and all products &
services have been fairly described. All prices are displayed
inclusive of GST, unless otherwise specified . Packaging or
delivery may vary from that shown. We have made every effort to
display as accurately as possible the products & services and
services that appear on the website/app/chatbot. To the extent
permitted by applicable law, CEDURA disclaims all warranties,
express or implied, as to the accuracy of the information
contained in any of the products & services or services on this
website/app/chatbot. CEDURA shall not be liable to any person for
any loss or damage which may arise from the use of any of the
information contained in any of the materials on this
website/app/chatbot.
All products & services/services and information displayed on
ceduratech.com ("Website/app/chatbot" or "ceduratech.com")
constitute an invitation to offer. Your order for purchase
constitutes your offer which shall be subject to the terms and
conditions as listed herein. ceduratech.com reserves the right to
accept or reject your offer in part or in full. Our acceptance of
your order will take place upon dispatch or delivery of the
product(s) or services(s) ordered. Dispatch of all the product(s)
or services(s) ordered, may or may not happen at the same time, in
such a scenario that portion of the order which has been
dispatched or deliveryed will be deemed to have been accepted by
ceduratech.com and the balance would continue to be on offer to
ceduratech.com and ceduratech.com reserves the right to accept or
reject such balance order. No act or omission of ceduratech.com
prior to the actual dispatch of the product (s) or services(s)
ordered will constitute acceptance of your offer.
Eligibility to Use
Use of the Website/app/chatbot is available only to persons who
can form legally binding contracts under applicable law. Persons
who are "incompetent to contract" within the meaning of the Indian
Contract Act, 1872 including un-discharged insolvents etc. are not
eligible to use the Website/app/chatbot. If your age is below 18
years you are prohibited to use/purchase/contract from/with this
website/app/chatbot. Such persons are also prohibited from
purchasing any material which is for adult consumption the sale or
purchase of which to/by minors are strictly prohibited.
ceduratech.com reserves the right to terminate your membership and
refuse to provide you with access to the website/app/chatbot if
ceduratech.com discovers that you are under the age of 18 years.
The website/app/chatbot is not available to persons whose
membership has been suspended or terminated by ceduratech.com for
any reason whatsoever. If you are registering as a business
entity, you represent that you have the authority to bind the
entity to this User Agreement. Unless otherwise specified, the
materials on this website/app/chatbot are directed solely at those
who access this web from India. ceduratech.com makes no
representation that any products & services or services referred
to in the materials on this web are appropriate for use, or
available outside India. Those who choose to access this
website/app/chatbot from outside India are responsible for
compliance with local laws if and to the extent local laws are
applicable. ceduratech.com will deliver the products & services or
services only within in India and will not be liable for any
claims relating to any products & services or services ordered
from outside India. Some Indian states prohibit direct sale of
merchandise from other states and require special documentation to
effect such a sale without dual taxation, if ceduratech.com
receives a order from such states or to be delivered to such
states (to see a list please refer our shipping policy) under such
circumstances ceduratech.com retains the right to accept or reject
the order.
Those who choose to access this website/app/chatbot from Indian
states which restrict such use are responsible for compliance with
local laws if and to the extent local state laws are applicable.
ceduratech.com will deliver the products & services or services
only within states having open import policy and will not be
liable for any claims relating to any products & services ordered
from restricted states.
Except where additional terms and conditions are provided which
are product or service specific, these terms and conditions
supersede all previous representations, understandings, or
agreements and shall prevail notwithstanding any variance with any
other terms of any order submitted. By using the services of
ceduratech.com you agree to be bound by the Terms and Conditions.
Account and registration obligations
Your Information is defined as any information you provide to us
in the registration, buying or listing process, in the feedback
area or through any e-mail feature or a written letter or form
mailed or submitted to any of our stores and offices. We will
protect your Information in accordance with our Privacy Policy .
If you use the Website/app/chatbot, you are responsible for
maintaining the confidentiality of your password and account and
any activities that occur under your account. CEDURA shall not be
liable to any person for any loss or damage which may arise as a
result of any failure by you to protect your password or account.
If you know or suspect that someone else knows your password or
suspect any unauthorised use of your password you should notify us
by contacting us immediately through the address provided in the
beginning of this agreement. If ceduratech.com has reason to
believe that there is likely to be a breach of security or misuse
of the ceduratech.com Website/app/chatbot, we may require you to
change your password or we may suspend your account without any
liability to ceduratech.com.
ceduratech.com does not want to receive confidential, proprietary
or trade secret information through this Website/app/chatbot
(excluding information related to any order you submit). Please
note that any information, materials, suggestions, ideas or
comments sent to ceduratech.com
ceduratech.com does not want to receive confidential, proprietary
or trade secret information through this Website/app/chatbot
(excluding information related to any order you submit). Please
note that any information, materials, suggestions, ideas or
comments sent to ceduratech.com will be deemed non-confidential.
By submitting any such information, you are granting
ceduratech.com an irrevocable and unrestricted license to use,
modify, reproduce, transmit, display and distribute such
materials, information, suggestions, ideas or comments for any
purpose whatsoever. However, we will not use your name in
connection with any such materials, information, suggestions, and
ideas or comments unless we first obtain your permission or
otherwise are required by law to do so
You also agree and confirm:
To provide true, accurate, current and complete information about
yourself as prompted by CEDURA registration form or guest details
form (such information being the "Registration Data").
To maintain and promptly update the Registration Data to keep it
true, accurate, current and complete. If you provide any
information that is untrue, inaccurate, incomplete, or not current
or if ceduratech.com has reasonable grounds to suspect that such
information is untrue, inaccurate, and not current or not in
accordance with the User Agreement, ceduratech.com has the right
to indefinitely suspend or terminate your membership and refuse to
provide you with access to the Website/app/chatbot.
That in the event that a non- delivery occurs on account of a
mistake by you (i.e. wrong name or address or any other wrong
information) any extra cost incurred by ceduratech.com for
redelivery shall be claimed from you and you shall pay such cost.
That you will use the services provided by ceduratech.com, its
affiliates, consultants and contracted companies, for lawful
purposes only and comply with all applicable laws and regulations
while using the Website/app/chatbot and transacting on the
Website/app/chatbot.
You will provide authentic and true information in all instances
where such information is requested of you. ceduratech.com
reserves the right to confirm and validate the information and
other details provided by you at any point of time. If upon
confirmation your details are found not to be true (wholly or
partly), ceduratech.com has the right in its sole discretion to
reject the registration and debar you from using the Services of
ceduratech.com and or other affiliated website/app/chatbot without
prior intimation whatsoever.
That you are accessing the services available on this
Website/app/chatbot and transacting at your sole risk and are
using your best and prudent judgment before entering into any
transaction through this Website/app/chatbot That the address at
which delivery of the product or services ordered by you is to be
made will be correct and proper in all respects.
That before placing an order you will check the product
description carefully. By placing an order for a product you agree
to be bound by the conditions of sale and invitation of offer
included in the item's description
Usage Restrictions
You shall not use the Website/app/chatbot for any of the following
purposes:
Disseminating any unlawful, harassing, libellous, abusive,
threatening, harmful, vulgar, obscene, or otherwise objectionable
material
Transmitting material that encourages conduct that constitutes a
criminal offence, results in civil liability or otherwise breaches
any relevant laws, regulations or code of practice.
Gaining unauthorised access to other computer systems.
Interfering with any other person's use or enjoyment of the
Website/app/chatbot.
Breaching any applicable laws;
Interfering or disrupting networks or website/app/chatbot
connected to the Website/app/chatbot.
Making, transmitting or storing electronic copies of materials
protected by copyright without the permission of the owner.
Pricing information
While ceduratech.com strives to provide accurate product and
pricing information, pricing or typographical errors may occur.
ceduratech.com cannot confirm the price of a product or service
until after you order. In the event that a product is listed at an
incorrect price or with incorrect information due to an error in
pricing or product information, ceduratech.com shall have the
right, at our sole discretion, to refuse or cancel any orders
placed for that product or service, unless the product has already
been dispatched. In the event that an item is mis-priced,
ceduratech.com may, at its discretion, either contact you for
instructions or cancel your order and notify you of such
cancellation. Unless the product or service ordered by you has
been dispatched, your offer will not be deemed accepted and
ceduratech.com will have the right to modify the price of the
product and contact you for further instructions using the e-mail
address provided by you during the time of registration, or cancel
the order and notify you of such cancellation. In the event that
ceduratech.com accepts your order the same shall be debited to
your credit / debit card account and duly notified to you by email
that the payment has been processed. The payment may be processed
prior to ceduratech.com dispatch or delivery of the product or
service that you have ordered. If we have to cancel the order
after we have processed the payment, the said amount will be
reversed back to your credit / debit card account.
GST
Reduced price will be inclusive of GST, unless specified.
In case of mispricing
Despite our best efforts, a small number of the many hundreds of
items in our catalogue are mispriced. However, we verify prices as
part of our dispatch procedures. If an item's correct price is
lower than our stated price, we charge the lower amount and send
you the item. If a product's correct price is higher than our
stated price, we will cancel your order and notify you of that
cancellation We strive to provide you with best value. However,
sometimes a price online may not match the price in a store in
your particular geographic region and store pricing may sometimes
differ from online prices. Prices and availability are subject to
change without notice
Cancellation by ceduratech.com
Please note that there may be certain orders that we are unable to
accept and must cancel. We reserve the right, at our sole
discretion, to refuse or cancel any order for any reason. Some
situations that may result in your order being canceled include
limitations on quantities available for purchase, inaccuracies or
errors in product or pricing information, or problems identified
by our credit and fraud avoidance department. We may also require
additional verifications or information before accepting any
order. We will inform you if all or any portion of your order is
canceled or if additional information is required to accept your
order. If your order is cancelled after your credit / debit card
has been charged, the said amount will be reversed back in your
Card
We will seek authorization on your Card for the aggregate amount
of the order placed by you, however, we may charge your card
(capture) only with the amount corresponding to the actual portion
of the order that we are able/willing to fulfill, and any
associated shipping charges/taxes and levies/or such etc. Any
surplus amount, for which we might have originally sought and
received an authorization on your card from your Card Issuer, if
not captured by us in the time period stipulated by our Merchant
Banker, will not be captured / charged. If however the same is
charged to your card / bank account in error, we will refund it as
soon as the same is realized by us or brought to our notice,
whichever is sooner. ceduratech.com reserves the right to capture
/ charge your card to the full or partial authorized amount for
the concerned order
Cancellation of fraudulent orders
To provide a safe and secure shopping experience, we regularly
monitor transactions for fraudulent activity. In the event of
detecting any suspicious activity, ceduratech.com reserves the
right to cancel pending and future orders without any liability.
ceduratech.com also reserves the right to refuse or cancel orders
in scenarios like inaccuracies in pricing of product on
website/app/chatbot and stock unavailability. We may also require
additional verifications or information before accepting any
order. If your order is cancelled after your card has been
charged, the said amount will be reversed to your Card Account.
Any promotional voucher used for the cancelled orders may not be
refunded.
Cancellations by the customer
You may cancel your order or some items in your order before we
bill and ship or deliver the items. You may also exchange the
merchandise or get a refund by returning the merchandise (with the
exception of perishables, made to order, or items of personal
hygiene such as under garments and cosmetics) in unused, saleable
condition in its original packaging along with original tags, for
a return or an exchange, within 14 days from the date on which
these goods are delivered. For details of how to exercise this
right please see our Returns Policy. ceduratech.com does not
accept returns or exchanges of jewellery, fragrances, cosmetics,
sunglasses, innerwear (under garments), swimwear, gift vouchers,
First Citizen Membership, mobile phones/ MP3 players, and any made
to order or altered merchandise. In case we receive a cancellation
notice and the order has not been processed /approved by us, we
shall cancel the order and refund the entire amount, if any,
charged to your card. However, orders placed for the First Citizen
Membership or gift vouchers cannot be canceled or returned. The
customer agrees not to dispute the decision made by ceduratech.com
and accept ceduratech.com decision regarding the cancellation.
Financial details
You agree, understand and confirm that the credit / debit card
details or other financial details provided by you for availing of
services on ceduratech.com will be correct and accurate and you
shall not use the credit /debit card or financial facility which
is not lawfully owned / obtained by you. You also understand that
any financial information submitted by you is directly received by
our acquiring bank and not stored by ceduratech.com.
ceduratech.com will not be liable for any credit / debit card
fraud. The liability for use of a card fraudulently will be on you
and the onus to 'prove otherwise' shall be exclusively on you. All
information collected by us shall be governed as per our Privacy
Policy
Electronic Communications
When you visit the Website/app/chatbot or send emails to us, you
are communicating with us electronically. You consent to receive
communications from us electronically. We will communicate with
you by email or by posting notices on the Website/app/chatbot. You
agree that all agreements, notices, disclosures and other
communications that we provide to you electronically satisfy any
legal requirement that such communications be in writing.
Reviews, feedback, submissions
All reviews, comments, feedback, postcards, suggestions, ideas,
and other submissions disclosed, submitted or offered to
ceduratech.com on or by this Website/app/chatbot or otherwise
disclosed, submitted or offered in connection with your use of
this Website/app/chatbot (collectively, the "Comments") shall be
and remain ceduratech.com property. Such disclosure, submission or
offer of any Comments shall constitute an assignment to
ceduratech.com of all worldwide rights, titles and interests in
all copyrights and other intellectual properties in the Comments.
Thus, ceduratech.com owns exclusively all such rights, titles and
interests and shall not be limited in any way in its use,
commercial or otherwise, of any Comments. ceduratech.com will be
entitled to use, reproduce, disclose, modify, adapt, create
derivative works from, publish, display and distribute any
Comments you submit for any purpose whatsoever, without
restriction and without compensating you in any way.
ceduratech.com is and shall be under no obligation (1) to maintain
any Comments in confidence; (2) to pay you any compensation for
any Comments; or (3) to respond to any Comments. You agree that
any Comments submitted by you to the Website/app/chatbot will not
violate this policy or any right of any third party, including
copyright, trademark, privacy or other personal or proprietary
right(s), and will not cause injury to any person or entity. You
further agree that no Comments submitted by you to the
Website/app/chatbot will be or contain libelous or otherwise
unlawful, threatening, abusive or obscene material, or contain
software viruses, political campaigning, commercial solicitation,
chain letters, mass mailings or any form of 'spam’.
ceduratech.com does not regularly review posted Comments, but does
reserve the right (but not the obligation) to monitor and edit or
remove any Comments submitted to the Website/app/chatbot. You
grant ceduratech.com the right to use the name that you submit in
connection with any Comments. You agree not to use a false email
address, impersonate any person or entity, or otherwise mislead as
to the origin of any Comments you submit. You are and shall remain
solely responsible for the content of any Comments you make and
you agree to indemnify ceduratech.com and its affiliates for all
claims resulting from any Comments you submit. ceduratech.com and
its affiliates take no responsibility and assume no liability for
any Comments submitted by you or any third party.
COPYRIGHT & TRADEMARK
ceduratech.com and its suppliers and licensors expressly reserve
all intellectual property rights in all text, programs, products &
services, processes, technology, content and other materials,
which appear on this Website/app/chatbot. Access to this
Website/app/chatbot does not confer and shall not be considered as
conferring upon anyone any license under any of ceduratech.com or
any third party's intellectual property rights. All rights,
including copyright, in this website/app/chatbot are owned by or
licensed to ceduratech.com. Any use of this website/app/chatbot or
its contents, including copying or storing it or them in whole or
part, other than for your own personal, non- commercial use is
prohibited without the permission of ceduratech.com. You may not
modify, distribute or re-post anything on this website/app/chatbot
for any purpose. The ceduratech.com names and logos and all
related product and service names, design marks and slogans are
the trademarks or service marks of CEDURA Limited. All other marks
are the property of their respective companies. No trademark or
service mark license is granted in connection with the materials
contained on this Website/app/chatbot. Access to this
Website/app/chatbot does not authorize anyone to use any name,
logo or mark in any manner.
References on this Website/app/chatbot to any names, marks,
products or services of third parties or hypertext links to third
party website/app/chatbot or information are provided solely as a
convenience to you and do not in any way constitute or imply
ceduratech.com endorsement, sponsorship or recommendation of the
third party, information, product or service. ceduratech.com is
not responsible for the content of any third party
website/app/chatbot and does not make any representations
regarding the content or accuracy of material on such
website/app/chatbot. If you decide to link to any such third party
website/app/chatbot, you do so entirely at your own risk.
All materials, including images, text, illustrations, designs,
icons, photographs, programs, music clips or downloads, video
clips and written and other materials that are part of this
Website/app/chatbot (collectively, the 'Contents') are intended
solely for personal, non- commercial use. You may download or copy
the Contents and other downloadable materials displayed on the
Website/app/chatbot for your personal use only. No right, title or
interest in any downloaded materials or software is transferred to
you as a result of any such downloading or copying. You may not
reproduce (except as noted above), publish, transmit, distribute,
display, modify, create derivative works from, sell or participate
in any sale of or exploit in any way, in whole or in part, any of
the Contents, the Website/app/chatbot or any related software. All
software used on this Website/app/chatbot is the property of
ceduratech.com or its suppliers and protected by Indian and
international copyright laws. The Contents and software on this
Website/app/chatbot may be used only as a shopping resource. Any
other use, including the reproduction, modification, distribution,
transmission, republication, display, or performance, of the
Contents on this Website/app/chatbot is strictly prohibited.
Unless otherwise noted, all Contents are copyrights, trademarks,
trade dress and/or other intellectual property owned, controlled
or licensed by ceduratech.com ,one of its affiliates or by third
parties who have licensed their materials to ceduratech.com and
are protected by Indian and international copyright laws. The
compilation (meaning the collection, arrangement, and assembly) of
all Contents on this Website/app/chatbot is the exclusive property
of ceduratech.com and is also protected by Indian and
international copyright laws
Objectionable material
You understand that by using this Website/app/chatbot or any
services provided on the Website/app/chatbot, you may encounter
Content that may be deemed by some to be offensive, indecent, or
objectionable, which Content may or may not be identified as such.
You agree to use the Website/app/chatbot and any service at your
sole risk and that to the fullest extent permitted under
applicable law, ceduratech.com and its affiliates shall have no
liability to you for Content that may be deemed offensive,
indecent, or objectionable to you.
INDEMNITY
You agree to defend, indemnify and hold harmless ceduratech.com,
its employees, directors, officers, agents and their successors
and assigns from and against any and all claims, liabilities,
damages, losses, costs and expenses, including attorney's fees,
caused by or arising out of claims based upon your actions or
inactions, which may result in any loss or liability to
ceduratech.com or any third party including but not limited to
breach of any warranties, representations or undertakings or in
relation to the non-fulfillment of any of your obligations under
this User Agreement or arising out of your violation of any
applicable laws, regulations including but not limited to
Intellectual Property Rights, payment of statutory dues and taxes,
claim of libel, defamation, violation of rights of privacy or
publicity, loss of service by other subscribers and infringement
of intellectual property or other rights. This clause shall
survive the expiry or termination of this User Agreement.
TERMINATION
This User Agreement is effective unless and until terminated by
either you or ceduratech.com. You may terminate this User
Agreement at any time by informing us in writing through Indian
postal system by registered post, that you no longer wish to be
associated with this website/app/chatbot, provided that you
discontinue any further use of this Website/app/chatbot.
ceduratech.com may terminate this User Agreement at any time and
may do so immediately without notice, and accordingly deny you
access to the Website/app/chatbot. Such termination will be
without any liability to ceduratech.com. Upon any termination of
the User Agreement by either you or ceduratech.com, you must
promptly destroy all materials downloaded or otherwise obtained
from this Website/app/chatbot, as well as all copies of such
materials, whether made under the User Agreement or otherwise.
ceduratech.com's right to any Comments shall survive any
termination of this User Agreement. Any such termination of the
User Agreement shall not cancel your obligation to pay for the
product already ordered from the Website/app/chatbot or affect any
liability that may have arisen under the User Agreement.
Limitation of liability and disclaimers
The Website/app/chatbot is provided without any warranties or
guarantees and in an "As Is" condition. You must bear the risks
associated with the use of the Website/app/chatbot.
The Website/app/chatbot provides content from other Internet
website/app/chatbot or resources and while ceduratech.com tries to
ensure that material included on the Website/app/chatbot is
correct, reputable and of high quality, it cannot accept
responsibility if this is not the case. ceduratech.com will not be
responsible for any errors or omissions or for the results
obtained from the use of such information or for any technical
problems you may experience with the Website/app/chatbot.
This disclaimer does not apply to any product warranty offered by
the manufacturer of the product as specified in the
productspecifications. This disclaimer constitutes an essential
part of this User Agreement.
To the fullest extent permitted under applicable law,
ceduratech.com or its suppliers shall not be liable for any
indirect, incidental, special, consequential or exemplary damages,
including but not limited to, damages for loss of profits,
goodwill, use, data or other intangible losses arising out of or
in connection with the Website/app/chatbot, its services or this
User Agreement.
Without prejudice to the generality of the section above, the
total liability of ceduratech.com to you for all liabilities
arising out of this User Agreement be it in tort or contract is
limited to the amount charged to you, against the value of the
products & services ordered by you. ceduratech.com its associates
and technology partners make no representations or warranties
about the accuracy, reliability, completeness, currentness and/or
timeliness of any content, information, software, text, graphics,
links or communications provided on or through the use of the
Website/app/chatbot or that the operation of the
Website/app/chatbot will be error free and/or uninterrupted.
Consequently, ceduratech.com assumes no liability whatsoever for
any monetary or other damage suffered by you on account of the
delay, failure, interruption, or corruption of any data or other
information transmitted in connection with use of the
Website/app/chatbot; and/or any interruption or errors in the
operation of the Website/app/chatbot.
By providing your phone number to us, You consent to be contacted
by us via phone calls and/or SMS notifications, in case of any
transactiona messages (i.e.) order, shipment delivery, returns,
refund related updates. If your phone number is registered under
the National Do Not Call Registry, we will not use your personal
information to initiate any promotional phone calls or promotional
SMS.
Website/app/chatbot security
You are prohibited from violating or attempting to violate the
security of the Website/app/chatbot, including, without
limitation,
Accessing data not intended for you or logging onto a server or an
account which you are not authorized to access;
Attempting to probe, scan or test the vulnerability of a system or
network or to breach security or authentication measures without
proper authorization;
Attempting to interfere with service to any other user, host or
network, including, without limitation, via means of submitting a
virus to the Website/app/chatbot, overloading, 'flooding,'
'spamming', 'mail bombing' or 'crashing;’
Sending unsolicited email, including promotions and/or advertising
of products & services or services; or Forging any TCP/IP packet
header or any part of the header information in any email or
newsgroup posting.
Violations of system or network security may result in civil or
criminal liability. ceduratech.com will investigate occurrences
that may involve such violations and may involve, and cooperate
with, law enforcement authorities in prosecuting users who are
involved in such violations. You agree not to use any device,
software or routine to interfere or attempt to interfere with the
proper working of this Website/app/chatbot or any activity being
conducted on this Website/app/chatbot. You agree, further, not to
use or attempt to use any engine, software, tool, agent or other
device or mechanism (including without limitation browsers,
spiders, robots, avatars or intelligent agents) to navigate or
search this Website/app/chatbot other than the search engine and
search agents available from ceduratech.com on this
Website/app/chatbot and other than generally available third party
web browsers (e.g., Netscape Navigator, Microsoft Internet
Explorer).
Entire agreement
If any part of this agreement is determined to be invalid or
unenforceable pursuant to applicable law including, but not
limited to, the warranty disclaimers and liability limitations set
forth above, then the invalid or unenforceable provision will be
deemed to be superseded by a valid, enforceable provision that
most closely matches the intent of the original provision and the
remainder of the agreement shall continue in effect. Unless
otherwise specified herein, this agreement constitutes the entire
agreement between you and ceduratech.com with respect to the
ceduratech.com website/app/chatbot/services and it supersedes all
prior or contemporaneous communications and proposals, whether
electronic, oral or written, between you and ceduratech.com with
respect to the ceduratech.com website/app/chatbot/services.
ceduratech.com's failure to act with respect to a breach by you or
others does not waive its right to act with respect to subsequent
or similar breaches.
Privacy policy
We do not sell or rent your personal information to third parties
for their marketing purposes without your explicit consent and we
only use your information as described in the Privacy Policy. We
view protection of your privacy as a very important community
principle. We understand clearly that you and your Information is
one of our most important assets. We store and process your
Information on computers located in India and abroad that are
protected by physical as well as technological security devices.
We use third parties to verify and certify our privacy principles.
If you object to your Information being transferred or used in
this way please do not use the Website/app/chatbot.
Governing law and jurisdiction
This User Agreement shall be construed in accordance with the
applicable laws of India. The Courts at Hyderabad shall have
exclusive jurisdiction in any proceedings arising out of this
agreement. Any dispute or difference either in interpretation or
otherwise, of any terms of this User Agreement between the parties
hereto, the same shall be referred to an independent arbitrator
who will be appointed by CEDURA Limited. and his decision shall be
final and binding on the parties hereto. The above arbitration
shall be in accordance with the Arbitration and Conciliation Act,
1996 as amended from time to time. The arbitration shall be held
in Mumbai. The High Court of judicature at Mumbai alone shall have
the jurisdiction and the Laws of India shall apply.
Modification of terms and conditions of service
ceduratech.com may at any time modify the User Agreement without
any prior notification to you. Subsequent to any modification of
the User Agreement, we will inform you of the modifications in the
User Agreement via e-mail at the address provided by you while
registering on ceduratech.com. You can access the latest version
of the User Agreement at any given time on ceduratech.com. You
should regularly review the User Agreement on ceduratech.com. In
the event the modified User Agreement is not acceptable to you,
you should discontinue using the service. However, if you continue
to use the service you shall be deemed to have agreed to accept
and abide by the modified User Agreement.